yixinxuxyz
2025 YMC Solutions
Problem 1
Compute the value of
\[\frac{2}{1+\frac{1+0}{1+\frac{1+2}{1+5}}}\]Solution: $\frac{2}{1+\frac{1+0}{1+\frac{1+2}{1+5}}}=\frac{2}{1+\frac{1+0}{1+\frac{1}{2}}}=\frac{2}{1+\frac{1}{\frac{3}{2}}}=\frac{2}{1+\frac{2}{3}}=\frac{2}{\frac{5}{3}}=2\cdot\frac{3}{5}=\boxed{\frac{6}{5}}$. $\square$
Problem 2
Cities $A$ and $B$ are connected by a highway 100 miles long. Alice sets out from city $A$ towards $B$ at a constant rate of 20 miles per hour, while Bob sets out from city $B$ at $150%$ the speed of Alice. When the two meet, Bob speeds up to a constant $n$ miles per hour, while Alice continues towards $B$ at the same rate as before. (As soon as Bob reaches $A$, he turns around and sets back towards $B$.) Given that the two reach city $B$ at the same time, what is the numerical value of $n$? Round your answer to the nearest tenth.
Solution: First, we calculate the speed of Bob to be $150\%\cdot20\text{ mph}=30\text{ mph}$. Their combined speed is thus $50\text{ mph}$, so that they meet after exactly $\frac{100}{50}=2$ hours at a place 60 miles from B.
From there, we see that the time it takes for Alice to travel 60 miles is equal to the time it takes Bob to travel $100+40=140$ miles. We set up the following porportion:
\[\frac{60}{140}=\frac{20}{n}\]Solving, we have $n=\frac{140}{3}\approx\boxed{46.7}$. $\square$
Problem 3
A right triangle has legs of length $20$ and $21$. A circle of radius $2$ rolls about the outside perimeter of the triangle, always keeping tangent at one point. Suppose the area of the region “swept-out” by (only!) the rolling circle can be represented in the form $a+b\pi$, where both $a$ and $b$ are positive integers. Find $a+b$.
Solution:
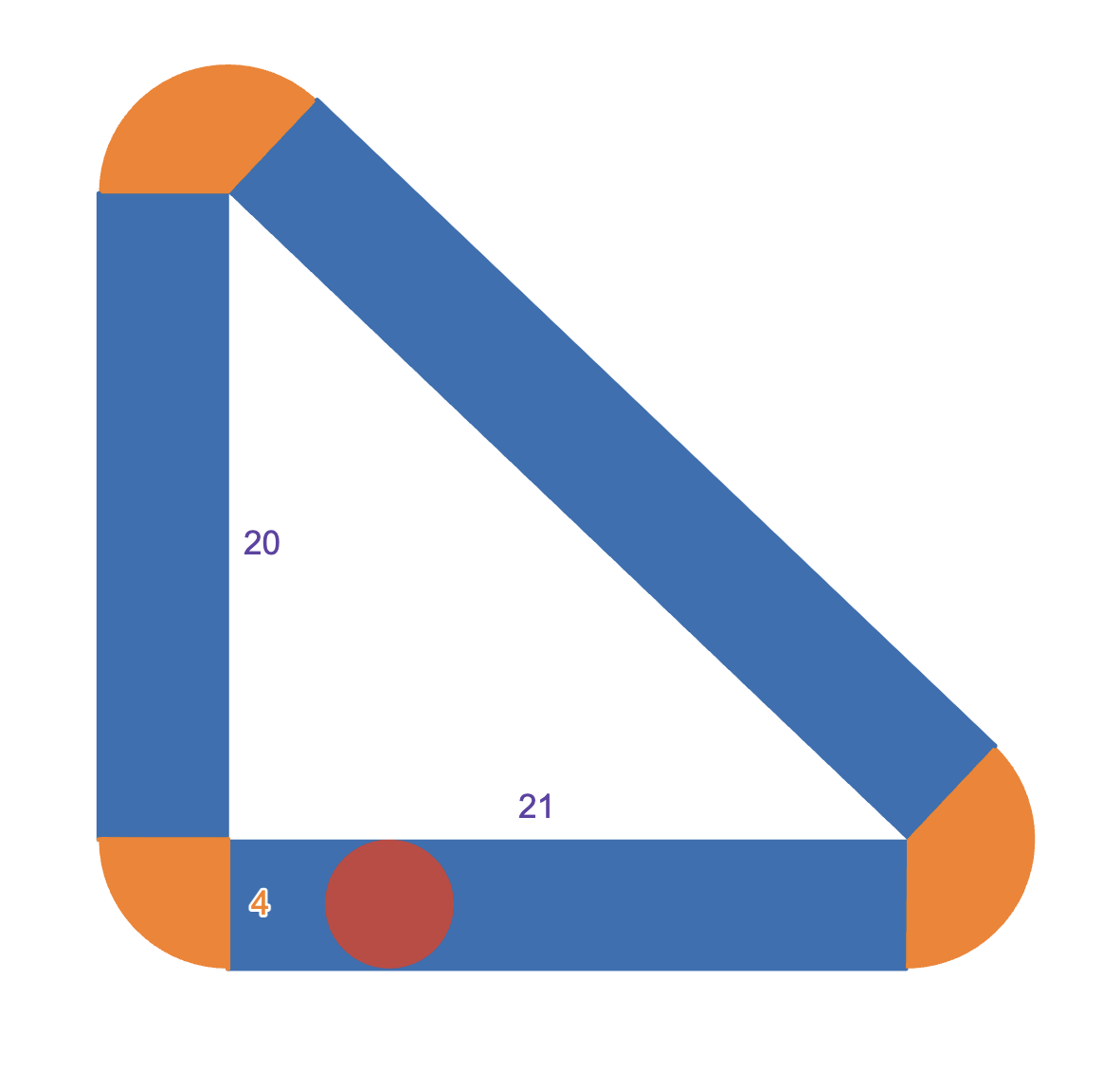
The desired area is shaded in orange and blue. Observe that the three orange sectors form in total a circle of radius $4$, while the three blue rectangles have dimensions $4\times20,4\times21,4\times29$. Thus, the area in question is
\[4(20+21+29)+\pi\cdot4^2=280+16\pi\]so that $a+b=280+16=\boxed{296}$. $\square$
Problem 4
A rigged coin is such that flipping 4 heads in a row is 4 times as likely as flipping 4 tails in a row. The probability that one flips 2 tails and 2 heads in some order can be represented as $m-n\sqrt{2}$ for positive integers $m$ and $n$. Find $m$.
Solution: Let the probability of flipping a head be $h>\frac{1}{2}$. Likewise, the probability of flipping a tail is $1-h$. Now, from the given, we have
\[\begin{gathered} h^4=4\cdot(1-h)^4\\ h=\sqrt{2}\cdot(1-h)\\ h(\sqrt{2}+1)=\sqrt{2}\\ h(\sqrt{2}+1)(\sqrt{2}-1)=(\sqrt{2}-1)(\sqrt{2}) \end{gathered}\]Thus, we find $h=2-\sqrt{2}.$ The desired probability is
\[\begin{aligned} \binom{4}{2}h^2(1-h)^2 &=6\big((2-\sqrt{2})(\sqrt{2}-1)\big)^2\\ &=6(3\sqrt2-4)^2\\ &=6(18+16-24\sqrt2)\\ &=204-144\sqrt{2} \end{aligned}\]So $m=\boxed{204}$. $\square$
Problem 5
Recall that the $n$th triangular number is defined to be the sum of the first $n$ positive integers. Similarly, define the $n$th tetrahedral number as the sum of the first $n$ triangular numbers. How many $k$ exist between $1$ and $100$ (inclusive) such that the $k$th tetrahedral number is divisible by $9$?
Solution: The formula for the $n$-th triangular number is well known to be $T_n={n+1\choose{2}}=\frac{(n)(n+1)}{2}$. Perhaps less well known is that the $n$-th tetrahedral number is given by $V_n={n+2\choose{3}}=\frac{(n)(n+1)(n+2)}{3}$. A proof can be found here.
Using this fact, we seek the number of $1\leq n\leq 100$ such that $9\vert\frac{(k)(k+1)(k+2)}{3}$; this is equivalent to $27\vert(k)(k+1)(k+2)$. Since $k,k+1,k+2$ must have different remainders $\pmod{3}$, it follows that exactly one of them must be divisble by 3. However, since the entire expression is divisible by $27=3^3$, one of $k,k+1,k+2$ must be a multiple of 27. The only such positive integer $k$ less than 100 are 25, 26, 27, 52, 53, 54, 79, 80, and 81: a total of $\boxed{9}$. $\square$
Problem 6
Let $S$ be the list of (possibly repeated) rational numbers formed such for each $10$-tuple of nonnegative integers $(a_1,a_2,a_3,\dots,a_{10})$, the number
\[n=\frac{1}{2^{a_1}3^{a_2}\cdots 11^{a_{10}}}\]is added to $S$. Find the sum of the elements in $S$.
For example, the number $\frac{1}{4}$ is a result from both tuples $(2,0,0,0,0\dots,0)$ and $(0,0,1,0,0,\dots,0)$ and thus appears twice in the list.
Solution: It can be seen that this product is exactly equal to
\[\begin{aligned} \prod_{m=2}^{11}\left(\sum_{n=0}^\infty\frac{1}{m^n}\right)&=\left(1+\frac{1}{2}+\frac{1}{4}+\dots\right)\left(1+\frac{1}{3}+\frac{1}{9}+\dots\right)\left(1+\frac{1}{4}+\frac{1}{16}+\dots\right)\cdots\left(1+\frac{1}{11}+\frac{1}{121}+\dots\right) \\ &=\frac{1}{1-\frac{1}{2}}\cdot\frac{1}{1-\frac{1}{3}}\cdot\frac{1}{1-\frac{1}{4}}\cdot\cdots\cdot\frac{1}{1-\frac{1}{11}}\\ &=\frac{2}{1}\cdot\frac{3}{2}\cdot\frac{4}{3}\cdot\cdots\cdot\frac{11}{10}\\ &=\boxed{11}. \end{aligned}\]If this isn’t immediately clear, consider the original problem statement. For any $n$, we are to select an arbitrary power of 2, then an arbitrary power of 3, … and an arbitrary power of 11. At this point, if we take the reciprocal, our number has exactly the form we desire: $n=\frac{1}{2^{a_1}3^{a_2}\cdots 11^{a_{10}}}$. Now, in the nested sum-product mentioned above, we see that in its expansion, we take an arbitrary term from the first factor $\left(1+\frac{1}{2}+\frac{1}{4}+\dots\right)$, then from the second factor, and so forth. Since each of these factors, in order, provides a factor of $2^x$,$3^x$,…, their product is exactly the equation we seek. $\square$
Problem 7
Triangle $ABC$ is right at angle $B$. The midpoints of $AB$ and $BC$ are denoted as $M$ and $N$. Segments $AN$ and $CM$ intersect at point $P$ such that $PM=4$ and $PN=3$. Compute the square of the length of hypotenuse $\overline{AC}$.
Solution:
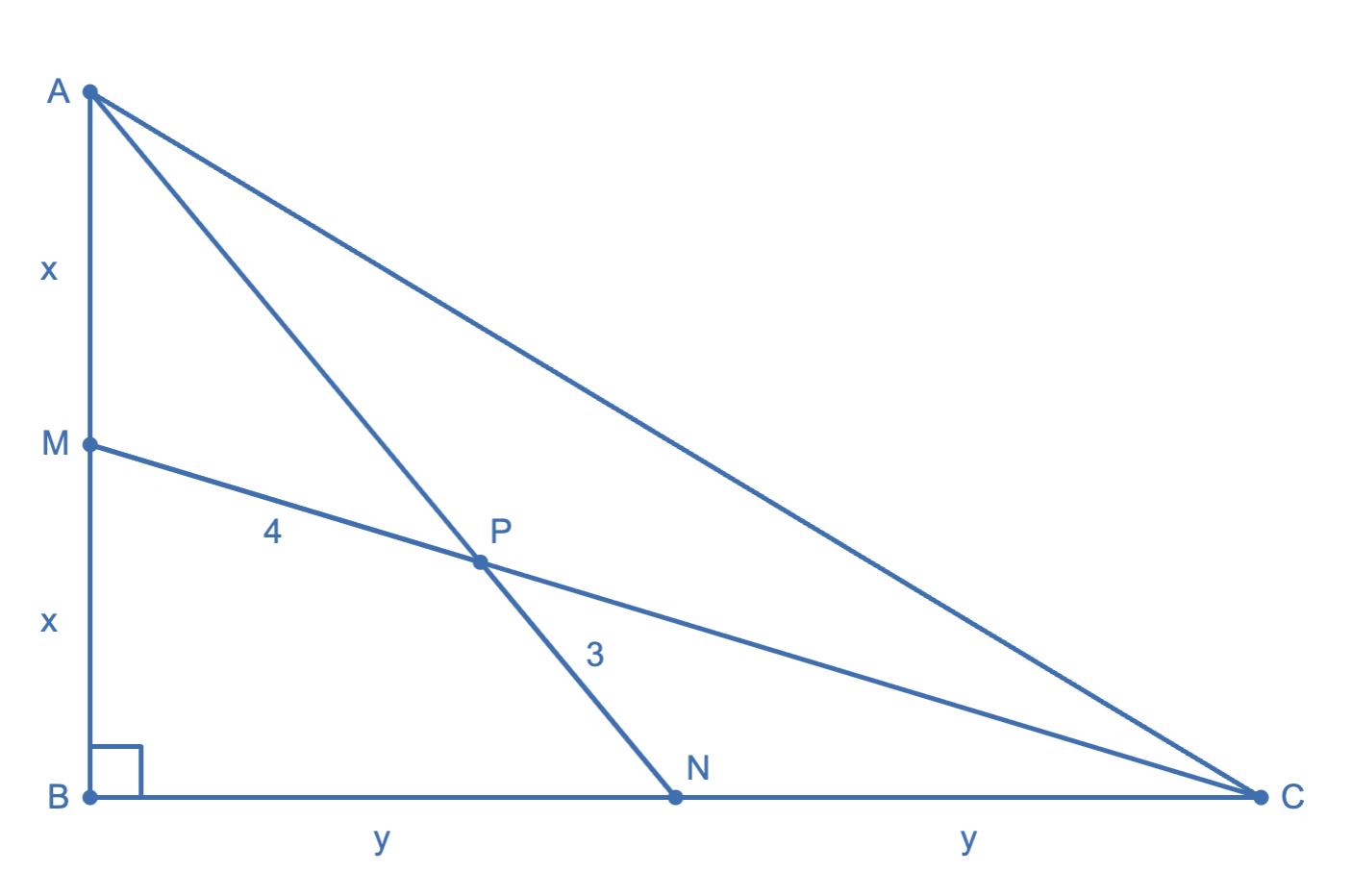
Let $AM=BM=x,BN=CN=y$. A property of the centroid $P$ is that $PC=2PM=8$; likewise, $PA=2PN=6$. Then, we have by the Pythagorean Theorem,
\[\begin{cases} x^2 + (2y)^2 = 12^2 \\ (2x)^2 + y^2 = 9^2 \\ (2x)^2+(2y)^2 = AC^2 \end{cases}\]Adding the first two equations yeilds $5x^2+5y^2=144+81=225$. Multiplying by $\frac{4}{5}$ on both sides yields the desired:
\[AC^2=4x^2+4y^2=\frac{4}{5}\cdot225=\boxed{180}.\blacksquare\]